ورقة بحثية جديدة من شركة Apple تحلل مشكلة تعطل دقة DeepSeek-R1

يُدرك مُستخدمو نموذج DeepSeek-R1 آلية تفكيره قبل إعطاء إجابة، وهذا أحد أسباب الاحترام الكبير الذي تحظى به نماذج الاستدلال الكبيرة (LRM، نموذج الاستدلال الكبير) بما في ذلك DeepSeek-R1.

ومع ذلك، شكك فريق من ستة باحثين من شركة Apple في هذا الأمر. فمن خلال تكليف النموذج بحل ألغاز مُختلفة، وجد فريق البحث أن دقة العديد من نماذج الاستدلال الكبيرة المُتطورة، مثل DeepSeek-R1 وo3-mini وClaude-3.7-Sonnet-Thinking، ستنهار تمامًا بعد تجاوز حد مُعين من التعقيد.

الشكل | أوراق بحثية ذات صلة (المصدر: https://ml-site.cdn-apple.com/papers/the-illusion-of-thinking.pdf)

تجدر الإشارة إلى أن سامي بنجيو، المدير الأول لأبحاث التعلم الآلي في شركة آبل، هو أحد مؤلفي هذه الورقة البحثية. وهو ليس فقط الشقيق الأصغر ليوشوا بنجيو، الحائز على جائزة تورينج، بل أيضًا أحد أوائل أعضاء فريق جوجل برين.

الشكل | المؤلفون الستة للورقة البحثية ذات الصلة، سامي بينجيو هو الثاني من اليمين (المصدر: خريطة البيانات)

خلص أحد مستخدمي الإنترنت على موقع X إلى أن آبل تصرفت كغاري ماركوس هذه المرة. في الواقع، نشر غاري ماركوس نفسه على لينكدإن تأكيدًا على ورقة آبل البحثية. كتب: "إن ورقة آبل الجديدة حول قدرات "الاستدلال" في نماذج اللغات الكبيرة مثيرة للإعجاب. سأشرح السبب (وأستكشف اعتراضًا محتملًا) في منشور طويل لنهاية الأسبوع لأُبيّن لماذا لا ينبغي أن يُفاجأ الناس كثيرًا." في "منشور نهاية الأسبوع الطويل" لغاري ماركوس، كتب: "هذه الورقة الجديدة من آبل تدعم انتقادي الخاص: حتى لو تجاوزت أحدث ما يُسمى بـ "نماذج الاستدلال" الإصدار o1، فإنها لا تزال غير قادرة على تحقيق استدلال موثوق من التوزيع في مسائل كلاسيكية مثل برج هانوي. هذه بلا شك أخبار سيئة للباحثين الذين يأملون أن "القدرة على الاستدلال" أو "الحوسبة أثناء الاستدلال" يمكن أن تُعيد نماذج اللغات الكبيرة إلى مسارها الصحيح وتتخلص من الإخفاقات المتكررة لتوسيع النطاق البسيط (الذي لم يتمكن أبدًا من إنتاج طفرة تكنولوجية تستحق اسم "GPT-5"). "

شكل | "مقال نهاية الأسبوع" بقلم غاري ماركوس على موقعه الشخصي (المصدر: https://garymarcus.substack.com/p/a-knockout-blow-for-llms)

إذن، هل هذه "أخبار سيئة" أم "أخبار جيدة"؟ لنبدأ بتفاصيل ورقة آبل.

يمكنه إكمال ما يصل إلى 100 إجراء صحيح، ولكن لا يمكنه إعطاء أكثر من 5 عمليات صحيحة

في الدراسة، وجد فريق البحث من Apple ثلاثة أوضاع استدلال مختلفة: في المهام منخفضة التعقيد، كان أداء نماذج اللغة الكبيرة القياسية أفضل من نماذج الاستدلال الكبيرة؛ وفي المهام متوسطة التعقيد، كان أداء نماذج الاستدلال الكبيرة أفضل؛ وفي المهام عالية التعقيد، لم يتمكن كلا النوعين من النماذج من إكمال المهمة بشكل فعال.

مع اقتراب المشكلة من التعقيد الحرج، ينخفض ​​الجهد المطلوب للاستدلال بشكل يخالف الحدس، مما يشير إلى أنه قد يكون هناك حد أعلى متأصل لتوسيع نطاق الحوسبة لنماذج الاستدلال الكبيرة.

تتحدى هذه الرؤى الافتراضات السائدة حول قدرات نماذج الاستدلال الكبيرة، وتشير إلى أن الأساليب الحالية قد تواجه عوائق جوهرية أمام تحقيق استدلال قابل للتعميم، كما يقول الفريق.

ومن الجدير بالذكر أن الفريق لاحظ قيودًا في نماذج الاستدلال الكبيرة في إجراء الحسابات الدقيقة. على سبيل المثال، عندما مُنحت النماذج خوارزمية لحل اللغز الرياضي "برج هانوي"، لم يتحسن أداؤها في هذه المسألة.

علاوة على ذلك، كشف التحليل المتعمق للأخطاء الأولى للنماذج عن أنماط سلوكية مفاجئة. على سبيل المثال، استطاعت النماذج إكمال ما يصل إلى 100 حركة صحيحة في لغز برج هانوي، ولكنها لم تتمكن من إكمال أكثر من خمس حركات صحيحة في لعبة المنطق والاستدلال River Crossing.

بشكل عام، يعتقد فريق البحث أن هذه الورقة تسلط الضوء على مزايا وعيوب نماذج التفكير واسعة النطاق الحالية، والاستنتاجات البحثية الرئيسية هي كما يلي:

أولاً، شكك فريق البحث في نموذج التقييم الحالي لنماذج التفكير واسعة النطاق على معايير رياضية راسخة، وصمم منصة اختبار تجريبية يمكن التحكم فيها باستخدام بيئة ألغاز خوارزمية.

ثانيًا، أظهرت تجارب فريق البحث أنه حتى أكثر نماذج التفكير واسعة النطاق تقدمًا (مثل o3-mini و DeepSeek-R1 و Claude-3.7-Sonnet-Thinking) لم تطور بعد قدرات حل المشكلات القابلة للتعميم. في بيئات مختلفة، عندما يتجاوز تعقيد المشكلة حدًا معينًا، ستنخفض دقتها في النهاية إلى الصفر.

ثالثًا، وجد فريق البحث أن نماذج التفكير واسعة النطاق لها حد توسع في قدرتها على التفكير يرتبط بتعقيد المشكلة، والذي يمكن تأكيده من خلال الاتجاه النزولي غير البديهي في عدد رموز الفكر بعد الوصول إلى نقطة تعقيد معينة.

رابعًا، شكك فريق البحث في نموذج التقييم الحالي القائم على الدقة النهائية. أظهر التحليل أنه مع زيادة تعقيد المشكلة، يظهر الحل الصحيح لاحقًا في عملية التفكير مقارنة بالحل غير الصحيح. خامسًا، كشف فريق البحث عن القيود المفاجئة لنماذج الاستدلال واسعة النطاق في قدرتها على إجراء حسابات دقيقة، بما في ذلك عدم قدرتها على الاستفادة من الخوارزميات الصريحة والتناقضات في الاستدلال عبر أنواع الألغاز المختلفة.

نماذج الاستدلال واسعة النطاق لديها قدرات محدودة على التصحيح الذاتي

ومن المفهوم أن نماذج الاستدلال واسعة النطاق هي متغيرات جديدة مشتقة من نماذج لغوية كبيرة الحجم تم تحسينها لمهام الاستدلال. هذه النماذج منتجات تكنولوجية جديدة، وتكمن سماتها الأساسية في آليات "التفكير" الفريدة، مثل سلسلة الأفكار ذاتية التأمل (CoT)، وقد أظهرت أداءً ممتازًا في العديد من معايير الاستدلال. يُمثل ظهور هذه النماذج نقلة نوعية محتملة في طريقة تعامل نماذج اللغات الكبيرة مع الاستدلال المعقد وحل المشكلات. ويعتقد بعض الباحثين أن هذا يمثل خطوة مهمة نحو قدرات ذكاء اصطناعي أكثر عمومية. على الرغم من هذه الرؤى والتطورات في الأداء، إلا أن المزايا والقيود الأساسية لنماذج الاستدلال الكبيرة لا تزال غير مفهومة تمامًا. السؤال الرئيسي الذي لا يزال دون إجابة هو: هل تعمم نماذج الاستدلال الكبيرة هذه قدرات الاستدلال، أم أنها ببساطة تستفيد من أشكال مختلفة من مطابقة الأنماط؟

كيف يتناسب أداؤها مع تعقيد المشكلة؟ وبالنظر إلى نفس الميزانية الحسابية لرموز الاستدلال، كيف تُقارن بنماذج اللغة الكبيرة القياسية التي لا "تفكر"؟

والأهم من ذلك، ما هي القيود المتأصلة في أساليب الاستدلال الحالية؟ وما التحسينات التي قد تكون ضرورية لتحقيق قدرات استدلال أكثر قوة؟

يعتقد فريق البحث أن قيود نموذج التقييم الحالي قد أدت إلى نقص في التحليل المنهجي لهذه المشكلات. تركز التقييمات الحالية بشكل أساسي على المعايير الرياضية الراسخة ومعايير الترميز. هذه المعايير قيمة بالتأكيد، ولكنها غالبًا ما تعاني من مشاكل تلوث البيانات ولا يمكنها توفير ظروف تجريبية خاضعة للرقابة في ظل سيناريوهات وتعقيدات مختلفة.

ولفهم سلوك التفكير لهذه النماذج بشكل أكثر دقة، يعتقد فريق البحث أن هناك حاجة إلى بيئة يمكن فيها إجراء تجارب خاضعة للرقابة.

ولهذه الغاية، بدلاً من استخدام معايير قياسية مثل مسائل الرياضيات، استخدموا بيئة ألغاز خاضعة للرقابة، أي عن طريق تعديل عناصر اللغز مع الاحتفاظ بالمنطق الأساسي، بحيث يمكن تغيير التعقيد بشكل منهجي، ويمكن فحص عملية الحل وعملية التفكير الداخلي.

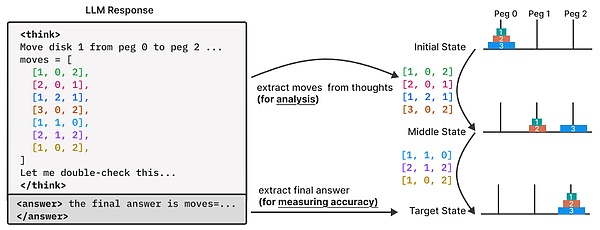
（المصدر: خريطة البيانات）

تتميز هذه الألغاز بالخصائص التالية:

(1) يمكنها توفير تحكم دقيق في التعقيد؛

(2) تتجنب التلوث الموجود عادةً في المعايير الحالية؛

(4) يدعم التقييم الدقيق القائم على المحاكاة، مما يتيح فحصًا دقيقًا للحلول وتحليلًا تفصيليًا للأخطاء.

من خلال البحث التجريبي، كشفوا عن العديد من النتائج الرئيسية حول نماذج التفكير الحالية واسعة النطاق:

أولاً، على الرغم من أن نماذج التفكير واسعة النطاق يمكنها تعلم آليات التأمل الذاتي المعقدة من خلال التعلم التعزيزي، إلا أنها فشلت في تطوير قدرات حل المشكلات القابلة للتعميم لمهام التخطيط، وينخفض ​​أداؤها إلى الصفر بعد تجاوز حد معين من التعقيد.

ثانيًا، كشفت مقارنة فريق البحث بين نماذج الاستدلال الكبيرة والنماذج الكبيرة القياسية في ظل حسابات الاستدلال المكافئة عن ثلاث آليات استدلال مختلفة.

الآلية الأولى هي أنه بالنسبة للمشكلات الأبسط والأقل تركيبية، يُظهر النموذج الكبير القياسي كفاءة ودقة أعلى.

الآلية الثانية هي أنه مع زيادة معتدلة في تعقيد المشكلة، يكتسب نموذج الاستدلال الكبير ميزة.

الآلية الثالثة هي أنه عندما تصبح المشكلة أكثر تعقيدًا مع زيادة العمق التركيبي، فإن كلا النوعين من النماذج يشهدان انهيارًا كاملاً في الأداء.

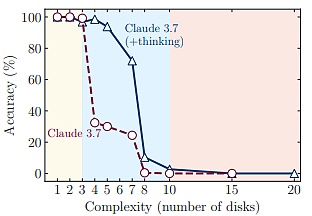
（المصدر: خريطة البيانات）

ومن الجدير بالذكر أنه عند الاقتراب من هذه النقطة الحرجة من الفشل، على الرغم من أن تشغيل نماذج الاستدلال الكبيرة بعيد عن الوصول إلى حد طول الجيل، إلا أنه مع زيادة تعقيد المشكلة، فإنها تبدأ في تقليل استثمار الاستدلال (الذي يتم قياسه من خلال عدد الرموز في الاستدلال).

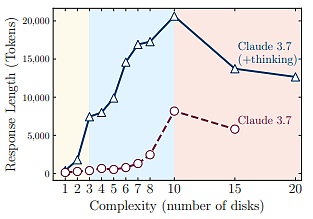
（المصدر: خريطة البيانات）

يُظهر هذا أن هناك قيدًا أساسيًا في قدرة نماذج الاستدلال الكبيرة على الاستدلال: سيزداد وقت استدلالها بشكل كبير مع نمو تعقيد المشكلة.

بالإضافة إلى ذلك، من خلال تحليل مسارات التفكير الوسيطة، اكتشف فريق البحث ظاهرة منتظمة تتعلق بتعقيد المشكلة، أي أنه في المشكلات الأبسط، يمكن لنموذج التفكير غالبًا العثور بسرعة على

الحل الخاطئ

, ولكن سيستمر النموذج في استكشاف الخيارات الخاطئة بكفاءة، وهو ما يُطلق عليه غالبًا "التفكير المفرط". في المسائل متوسطة التعقيد، يحتاج النموذج إلى استكشاف مُكثّف لعدد كبير من المسارات الخاطئة قبل أن يجد الحل الصحيح. عند تجاوز حدّ مُعيّن من التعقيد، يعجز النموذج تمامًا عن إيجاد الحل الصحيح. صرّح باي تينغ، الأستاذ المُشارك في جامعة بكين للبريد والاتصالات، لموقع DeepTech بأنه على غرار طريقة تفكير البشر، بالنسبة للمسائل المُعقدة، ورغم أننا لا نعرف الإجابة الصحيحة، فإننا غالبًا ما نعرف ما هو الخطأ. ويرتبط هذا تحديدًا بحجم مساحة الحل. غالبًا ما تكون مساحة الحل للمسائل البسيطة في مُقدّمة مسار التفكير، نظرًا لقصر السلسلة المنطقية وتوافق الميزات العالي. أما بالنسبة للمسائل المُعقدة، فتتوسع مساحة الحل بشكل مُتزايد لأنها تتضمن اقترانًا مُتغيرًا متعدد الأبعاد وتداخلًا هرميًا منطقيًا. مساحة الحل واسعة، وهو ما يتجلى موضوعيًا كوضع لاحق نسبي في تسلسل التفكير.

ماذا يحدث داخل "تفكير" نموذج التفكير؟

في الدراسة، أُجريت معظم التجارب على نماذج التفكير ونماذجها غير التفكيرية المقابلة، مثل Claude 3.7 Sonnet (مع/بدون تفكير) وDeepSeek-R1/V3. اختار فريق البحث هذه النماذج لأنها، على عكس نماذج مثل سلسلة O من OpenAI، تتيح الوصول إلى رموز التفكير.

لكل نموذج من الألغاز، أنتج فريق البحث 25 عينة وأبلغ عن متوسط ​​أداء كل نموذج.

ولتعميق فهم عملية التفكير في نماذج التفكير، أجرى فريق البحث تحليلًا مفصلًا لآثار تفكيرها. خلال هذه الفترة، بنوا بيئة تجريبية للألغاز لتحقيق تحليل متعمق يتجاوز الإجابة النهائية للنموذج، حتى يتمكنوا من ملاحظة وتحليل آثار التفكير (أي "عملية التفكير") الناتجة عنه بطريقة أكثر تفصيلاً. وبشكل أكثر تحديدًا، استخرجوا وحلّلوا الحلول الوسيطة التي تم استكشافها خلال عملية تفكير النموذج بمساعدة محاكي الألغاز. ثم فحصوا أنماط وخصائص هذه الحلول الوسيطة، وصحتها بالنسبة لموضعها التسلسلي في عملية التفكير، وكيف تطورت هذه الأنماط مع تزايد تعقيد المشكلة. في هذا التحليل، ركز فريق البحث على آثار التفكير التي أنتجها نموذج التفكير "سونيت كلود 3.7" في تجربة مجموعة الألغاز. بالنسبة لكل حل وسيط تم تحديده في التتبع، سجل فريق البحث ما يلي: (1) موقعه النسبي في تتبع التفكير (الموحد بطول الفكر الإجمالي)، (2) صحته التي تم التحقق منها بواسطة محاكي الألغاز الخاص بفريق البحث، و(3) تعقيد المشكلة المقابلة. سمح هذا لفريق البحث بوصف تقدم ودقة تشكيل الحل طوال عملية التفكير. وجد فريق البحث أنه في المسائل البسيطة، عادةً ما يجد نموذج الاستدلال الحل الصحيح في مرحلة مبكرة من عملية التفكير، ثم يواصل استكشاف الحلول الخاطئة. بالمقارنة مع الحل الصحيح (الأخضر)، يتغير توزيع الحلول الخاطئة (الأحمر) بشكل ملحوظ نحو نهاية سلسلة التفكير. ومع ازدياد تعقيد المسألة بشكل معتدل، ينعكس هذا الاتجاه: يستكشف النموذج الحلول الخاطئة أولاً، ويصل غالبًا إلى الحل الصحيح في المراحل اللاحقة من التفكير. هذه المرة، أصبح توزيع الحلول غير الصحيحة (الأحمر) أكثر تحولاً إلى الأسفل مقارنة بالحل الصحيح (الأخضر).

وأخيرًا، بالنسبة للمشكلات ذات التعقيد الأعلى، يبدأ النموذج في الانهيار، مما يعني أن النموذج غير قادر على توليد أي حلول صحيحة أثناء عملية التفكير.

يقدم الشكل التالي تحليلًا إضافيًا لدقة الحلول داخل أجزاء تسلسل الفكر (الفواصل الزمنية) في بيئة برج هانوي.

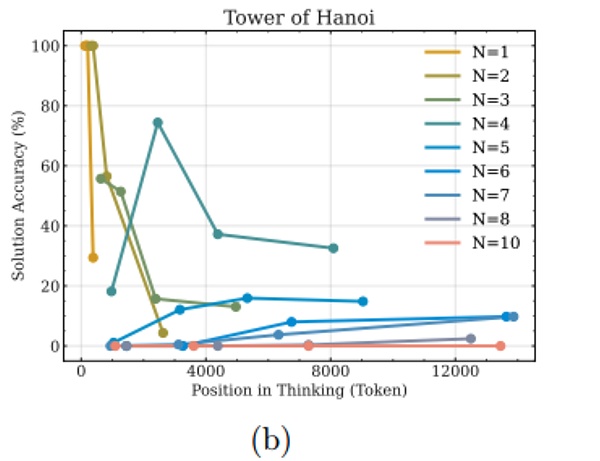
يمكن ملاحظة أنه بالنسبة للمشكلات الأبسط (القيم الأصغر لـ N)، تميل دقة الحل إلى الانخفاض أو التقلب مع تقدم التفكير، مما يوفر دليلاً إضافيًا على ظاهرة الإفراط في التفكير.

ومع ذلك، بالنسبة للمسائل الأكثر تعقيدًا، يتغير هذا الاتجاه - حيث تزداد دقة الحل مع تقدم التفكير حتى يصل إلى حد معين. بعد هذا الحد من التعقيد، في "وضع التعطل"، تكون دقة النموذج صفرًا.

صرح باي تينغ لـ DeepTech أن النموذج يحتاج إلى التفكير عدة مرات في المسائل المعقدة. ونظرًا لعدم وجود حل صحيح، قد تتبنى آلية التفكير في النموذج استراتيجية لتحسين كفاءة توليد التفكير التكراري المتعدد، والتي قد تكون استراتيجية لحماية الموارد لمنع تكرارها أكثر من اللازم. لذلك، يجب تحليل نتائج هذه الورقة بعناية والتحقق منها من مستوى تطبيق النموذج.

وأشار باي تينغ إلى أنه من الممكن أيضًا أن تكون عملية التفكير في النماذج الكبيرة بمثابة استدعاء لوضع الذاكرة. بالنسبة لنماذج مثل DeepSeek-R1 وo3-mini، يعتمد أداؤها بشكل كبير على تغطية أوضاع الذاكرة في بيانات التدريب. عندما يتجاوز تعقيد المشكلة حد تغطية وضع الذاكرة (مثل بيئة الألغاز القابلة للتحكم التي صممها فريق بحث Apple هذه المرة)، يقع النموذج في حالة "دقة صفرية".

مع أن بيئة الألغاز تسمح بإجراء تجارب مُتحكم بها مع تحكم دقيق في تعقيد المشكلة، إلا أنها لا تمثل سوى مجموعة فرعية صغيرة من مهام التفكير المنطقي، وقد لا تعكس تنوع مشاكل التفكير المنطقي الواقعية أو التي تتطلب معرفة مكثفة.

تجدر الإشارة إلى أن هذه الدراسة تعتمد بشكل أساسي على وصول واجهة برمجة التطبيقات (API) إلى نماذج التفكير المنطقي الكبيرة ذات الحدود المغلقة، وهو قيد يمنع فريق البحث من تحليل حالتها الداخلية أو مكوناتها الهيكلية.

بالإضافة إلى ذلك، عند استخدام مُحاكي ألغاز حتمي، افترض فريق البحث أنه يمكن التحقق من التفكير المنطقي بدقة خطوة بخطوة. ومع ذلك، في المجالات الأقل هيكلية، قد يكون من الصعب تحقيق هذا التحقق الدقيق، مما يحد من تطبيق أسلوب التحليل هذا على نطاق أوسع من سيناريوهات الاستدلال. باختصار، درس فريق البحث نماذج الاستدلال ذات الحدود الكبيرة من منظور تعقيد المشكلة من خلال بيئة ألغاز مُتحكم بها. تكشف هذه النتيجة عن قيود النماذج الحالية: فرغم آليات التأمل الذاتي المعقدة، لا تزال هذه النماذج غير قادرة على تطوير قدرات استدلال قابلة للتعميم بعد تجاوز حد معين من التعقيد. يعتقد فريق البحث أن هذا الإنجاز قد يُمهد الطريق لدراسة قدرة هذه النماذج على الاستدلال.